Column 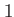 |
Column 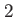 |
Column 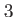 |
Column 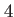 |
Column 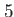 |
Column 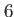 |
Column 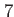 |
Column 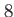 |
N of integration step of integration step |
Time 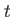 |
Execution time |
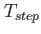 |
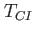 |
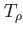 |
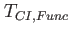 |
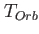 |
this table displays the column structure of the Timing.dat output file. Here,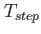 is the execution time for the present integration step, is the execution time for the present integration step,
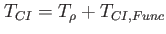 is the overall execution time in this step spent on the configuration interaction, i.e., the coefficients part of the program. is the overall execution time in this step spent on the configuration interaction, i.e., the coefficients part of the program. 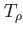 is the runtime consumed to invert the matrix elements of the reduced one-body density, is the runtime consumed to invert the matrix elements of the reduced one-body density,
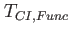 is the execution time consumed in applying the Hamiltonian to the coeffcients vector. is the execution time consumed in applying the Hamiltonian to the coeffcients vector. 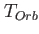 , finally, is the execution time spent for evaluating the right hand side of the orbitals' equations. , finally, is the execution time spent for evaluating the right hand side of the orbitals' equations.
|