PRA: crystallisation via cavity mediated interactions

In quantum mechanics, particles can be divided into bosons and fermions depending on their exchange statistics. Bosons can be swapped arbitrarily, while swapping two fermions produces a phase of minus one. This gives rise to very different density distributions. Bosons can occupy the same quantum mechanical state as exemplified in the famous Bose-Einstein condensation, where all the particles coalesce in the same quantum state and acquire macroscopic characteristics. Fermions instead obey the Pauli exclusion principle, whereby they can never occupy the same state and can therefore never condense (they instead tend to form lattice structures).

When we confine quantum gases in lower-dimensional setups, however, things become more fuzzy. A gas of bosons with strong contact repulsions confined in one dimension (a so-called Tonks-Girardeau gas) can “fermionize” and mimic the Pauli principle: the bosonic real-space density distribution becomes indistinguishable from that of free fermions. To achieve the strong repulsions necessary to trigger fermionization, some sort of confinement is typically used, such as with optical lattices obtained by using standing waves of lasers. Things become even more interesting when the repulsions are long ranged, as in the case of dipolar particles. In a gas of dipolar bosons, for instance, the short-range part of the interactions pushes the particles first into a Tonks-Girardeau state. When the interaction strength is increased further, the long-range part impacts also the momentum-space density distribution, giving it fermionic character.

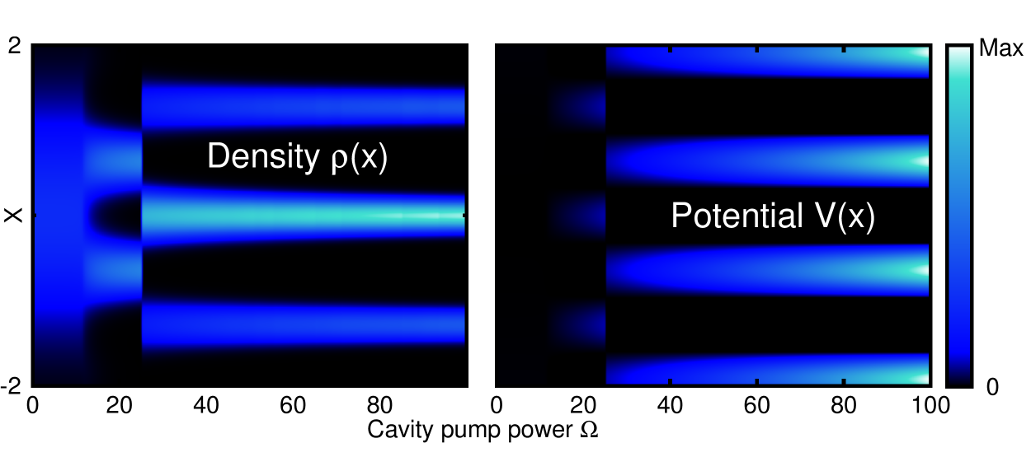
In our work, we achieved a completely new route to fermionization by using infinite-range interactions that are mediated by photons in an optical cavity. The basic mechanism of operation is rather straightforward: if we place a Bose-Einstein condensate in a cavity (egbetween two highly reflective mirrors) and shine a laser onto it, the photons will scatter on the atoms. The geometry of the setup can be chosen such that most of the light scatters within the cavity. Once the light gets reflected at the boundaries of the cavity, the scattering process can repeat itself. The photons can therefore couple with many different atoms many times. The effect is that the atoms will interact with each other through the mediation of the photons, and because of the many roundtrips of the light within the cavity, this interaction can be modelled as being infinite-ranged. The strength of the external laser then controls the intensity of the interactions.

In our work, we used MCTDH-X to simulate the cavity-atom system and solve the many-body Schrödinger equation to obtain its ground state properties. We found that, as the intensity of the external laser (and correspondingly the cavity-mediated interaction strength) is progressively increased, the bosons do indeed fermionize. In contrast to dipolar gases, however, in this case the fermionization of both real and momentum space observables happens simultaneously. Our approach also shows a very exciting interplay between contact and infinite-range interactions. It is possible to reduce the strength of the contact interactions needed to trigger fermionization by one order of magnitude if the cavity-mediated interactions are increased accordingly!

We expect the implementation of fermionization with cavities to have many other practical advantages. The cavity setup can be experimentally more flexible. It is for instance amenable to extensions to a multimode configuration. A multimode cavity set-up would shift the interaction range from infinite towards long-range, and would allow to investigate the effect of tuning the interaction range. As mentioned above, typical fermionization experiments use an optical lattice to artificially increase the interactions between the bosons. In our setup, as the interactions are instead mediated by the cavity, the optical lattice becomes superfluous. This means that it could instead be employed to investigate other phenomena with greater flexibility. For instance, by using a lattice incommensurate with the cavity wavelength, one could probe the interplay between fermionization and quasiperiodic structures. In a system where the pump wavelength is incommensurate with an additional optical lattice along the cavity direction it is namely possible to realize a Bose glass phase, an insulating state that contains rare “puddles” of superfluidity.

Read more on Physical Review A or on the arxiv.

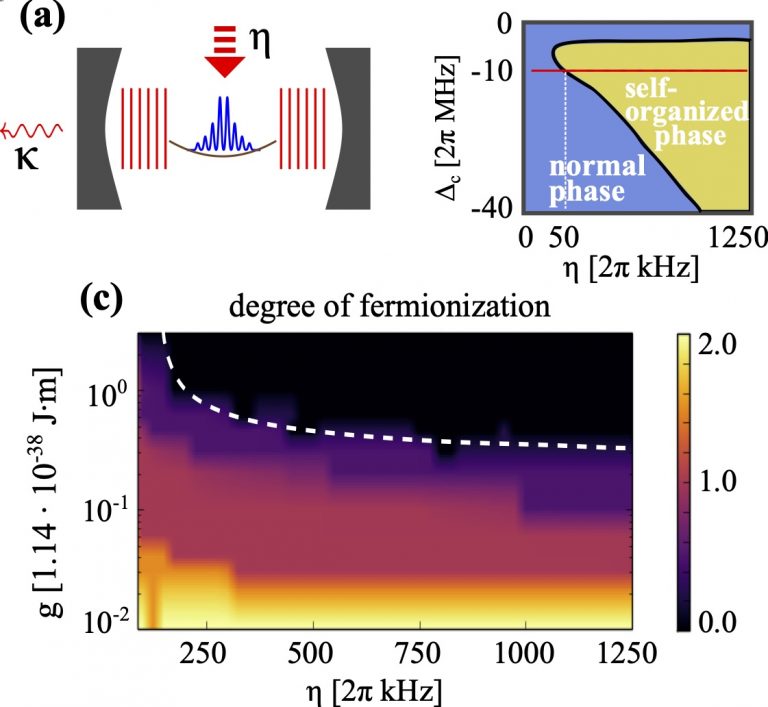
(a) The cavity setup of our simulations: a Bose-Einstein condensate (blue) is placed into a high-finesse optical cavity (grey) and irradiated with an external laser (thick red arrow). Some of the photons scatter within the cavity (red vertical lines) and create effective infinite-range interactions between the atoms. (b) Sketch of the phase diagram of the system as a function of laser intensity η and cavity detuning Δ_c (the fermionization regime appears at large values of η). (c) Onset of fermionization (black region) as a function of laser intensity η and particle contact interaction strength g.