PRA: accuracy of quantum simulators
Ultracold quantum simulators are used to recreate, i.e. simulate, the environment of a target quantum system with ultracold atoms. The atoms play the roles of the quantum particles we want to simulate. Optical laser traps can be used to spatially localize the atoms around discrete sites and introduce an effective lattice structure. Their interactions can be controlled, too, for instance with magnetic fields via Feshbach resonances. To obtain information about the system, we can shine a laser onto it and analyze the light that comes out. Whereas the original system is typically hard to realize directly in experiments or study with computational methods, ultracold quantum simulators consist of very stable and controllable components. This allows us for instance to realize lattices with no manufacturing defects, where the positions of each site and the interactions between the particles can be controlled with extreme precision, and where measurements are much easier to perform. Another advantage of quantum simulators is that they are, in principle, scalable to much larger systems that can be possibly simulated with classical computations. The fast development of quantum simulators also raises the fundamental issue of their accuracy and validity. If we want to make sure that they realize the target toy model and not a different one, we need to calibrate the parameters correctly. Furthermore, there might be regimes of the target quantum system that simply cannot be achieved with the quantum simulators because of technical limitations (not strong enough lasers, not dilute enough gases, or secondary processes between the actors that cannot be suppressed). For instance, it is known that the validity of quantum simulation can become reduced when the particles become strongly interacting, specially if the spatial range of such interactions is large.
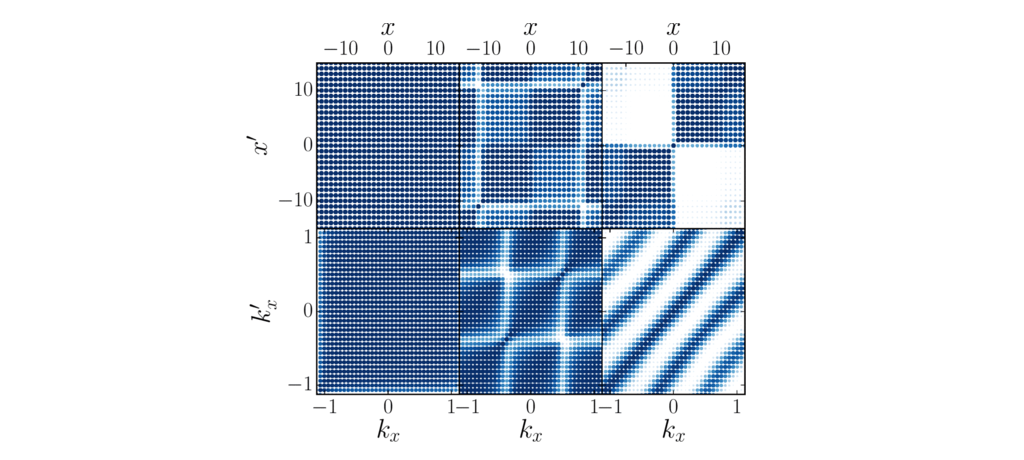
In our recent work, we addressed precisely these questions with the concrete example of simulating a one-dimensional dipolar Bose-Hubbard model, in which bosons interact on a lattice via longer-ranged dipole-dipole interactions. These are the interactions that emerge between electric dipoles, i.e. particles with spatially separate positive and negative electric charges. Since electrons in solids interact via Coulomb interactions, which are also long-ranged, dipolar Hubbard and Bose-Hubbard models have the potential of providing an accurate description of the physics underpinning real high-temperature superconductors. One way to quantum simulate the dipolar Bose-Hubbard model is by employing ultracold polar molecules instead of ultracold atoms. NaCs (“Sodium-Caesium”) mixtures provide an excellent platform for this. NaCs are bialkali molecules formed of magnetoassociated sodium and caesium atoms and have one of the largest dipole moments currently achievable in experiments. In our paper, we studied the regime of validity of an ultracold quantum simulator composed of a one-dimensional gas of dipolar bosons like NaCs molecules in an optical lattice. We did so by running numerical simulations of both the quantum simulator itself, described as a continuum system with the software MCTDH-X, and the lattice toy model obtained by employing the QuSpin python library. We performed a full quantitative comparison between the continuum and the lattice descriptions by not only comparing energies and density distributions, but also by calculating direct overlaps between the continuum and lattice many-body wave functions. This allowed us to directly compare very different descriptions of the same phenomenon.
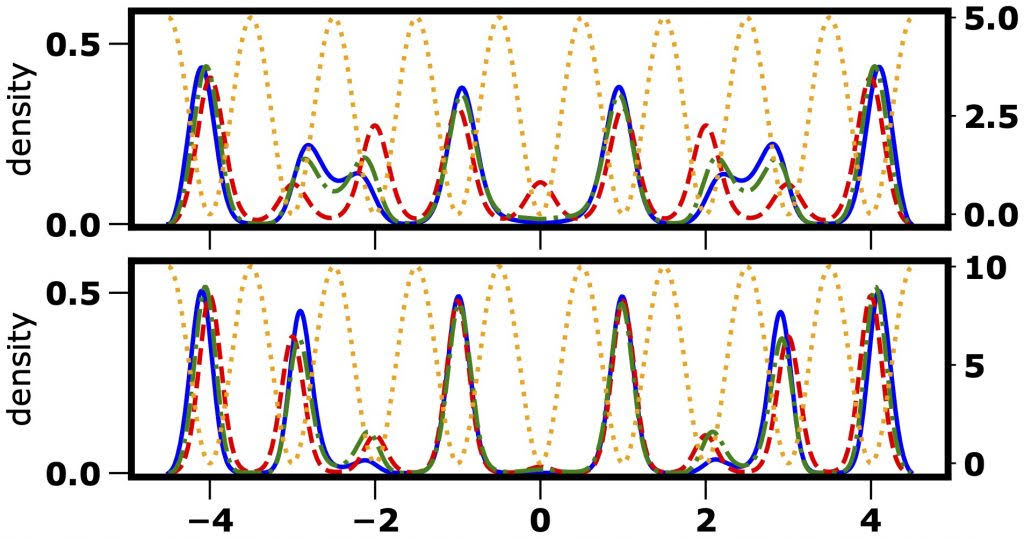
Our results show that in regimes of strong dipole-dipole interactions and high densities the continuum system indeed fails to recreate the desired single-band Bose-Hubbard lattice model. The discrepancy is not just quantitative, but also qualitative. For instance, whereas the single-band Bose-Hubbard model should have particles in the center of the lattice (see figure), the quantum simulator exhibits empty sites. Two-band Bose-Hubbard models become necessary to reduce the discrepancy, but quantitative deviations in the density profile still remain. This indicates that the quantum simulator is actually simulating a Bose-Hubbard model with many more bands than what we expected. Our study highlights the role of strong dipole-dipole interactions in generating physics beyond lowest-band descriptions, and demonstrates that such regimes require careful considerations when benchmarking the validity of quantum simulators. Furthermore, it offers a blueprint for a full-scale, quantitative analysis between continuum and lattice methods, since our analysis can be applied to more general ultracold quantum systems. In the future, we plan to extend our analysis to more diverse kinds of quantum simulators, for instance in two or three dimensions or with attractive interactions instead of repulsive ones.