Quantum Simulation of Crystal Formation with Ultracol Dipolar Bosons

The quantum properties underlying crystal formation can be replicated and investigated with the help of ultracold atoms. Our recent paper in Physical Review Letters shows how the use of dipolar atoms enables even the realization and precise measurement of structures that have not yet been observed in any material.

Crystals are ubiquitous in nature. They are formed by many different materials – from mineral salts to heavy metals like bismuth. Their structures emerge because a particular regular ordering of atoms or molecules is favorable, because it requires the smallest amount of energy. A cube with one constituent on each of its eight corners, for instance, is a crystal structure that is very common in nature. A crystal’s structure determines many of its physical properties, such as how well it conducts a current or heat or how it cracks and behaves when it is illuminated by light. But what determines these crystal structures? They emerge as a consequence of the quantum properties of and the interactions between their constituents, which, however, are often scientifically hard to understand and also hard measure.

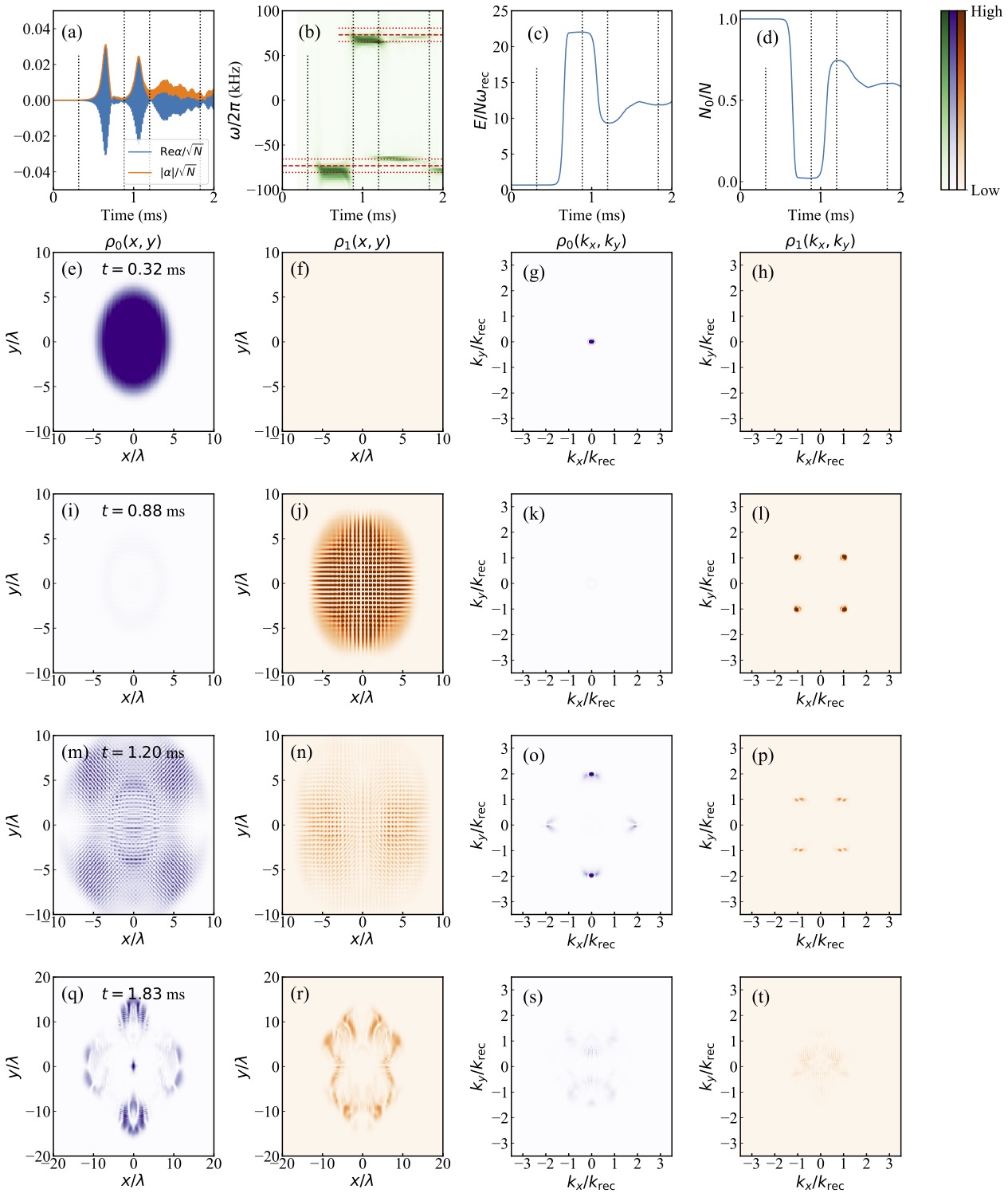
To nevertheless get to the bottom of the quantum properties of the formation of crystal structures, scientists can simulate the process using Bose-Einstein condensates – trapped ultracold atoms cooled down to temperatures close to absolute zero or minus 273.15 degrees Celsius. The atoms in these highly artificial and highly fragile systems are extremely well under control. With careful tuning, the ultracold atoms behave exactly as if they were the constituents forming a crystal. Although building and running such a quantum simulator is a more demanding task than just growing a crystal from a certain material, the method offers two main advantages: First, scientists can tune the properties for the quantum simulator almost at will, which is not possible for conventional crystals. Second, the standard readout of cold-atom quantum simulators are images containing information about all crystal particles. For a conventional crystal, by contrast, only the exterior is visible, while the interior – and in particular its quantum properties – is difficult to observe.

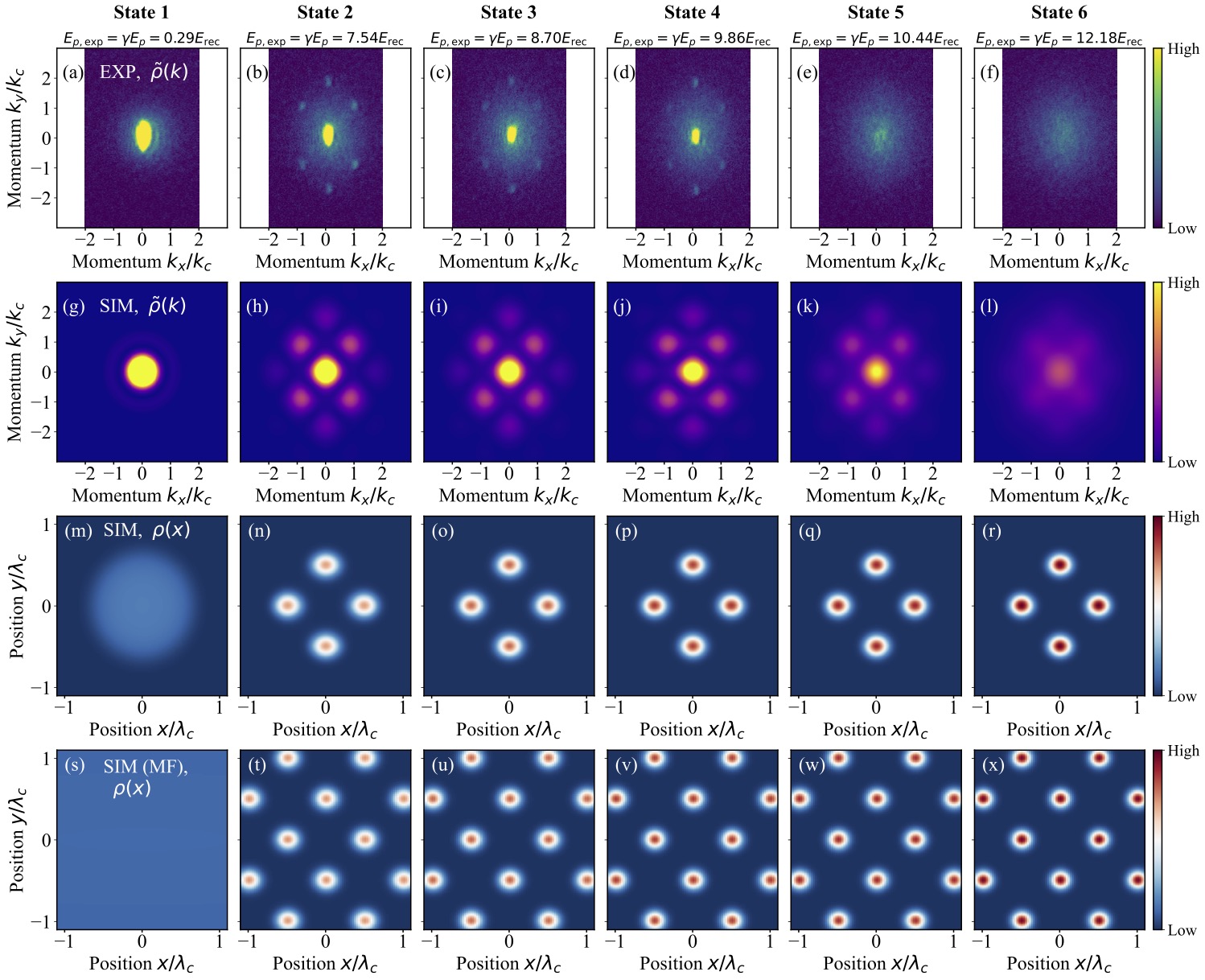
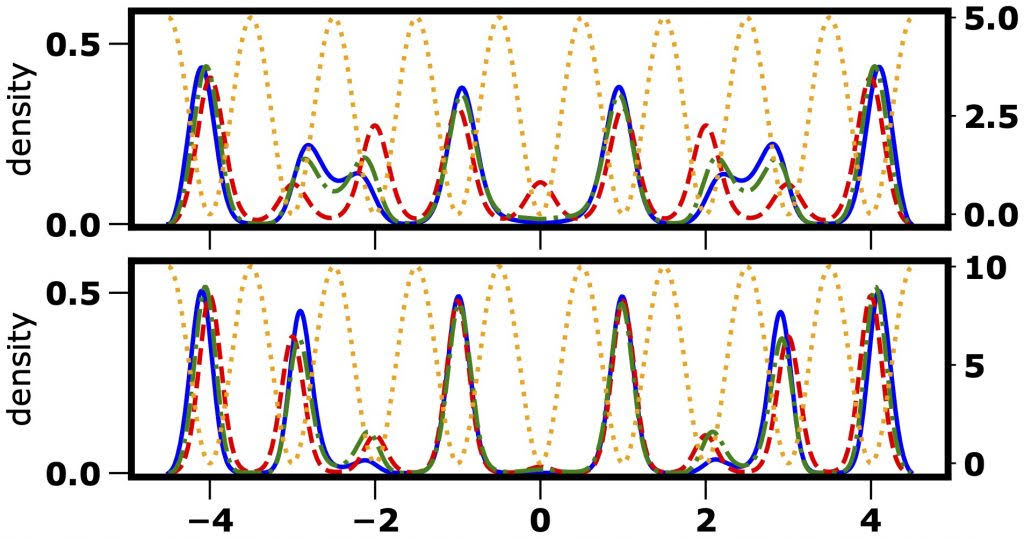
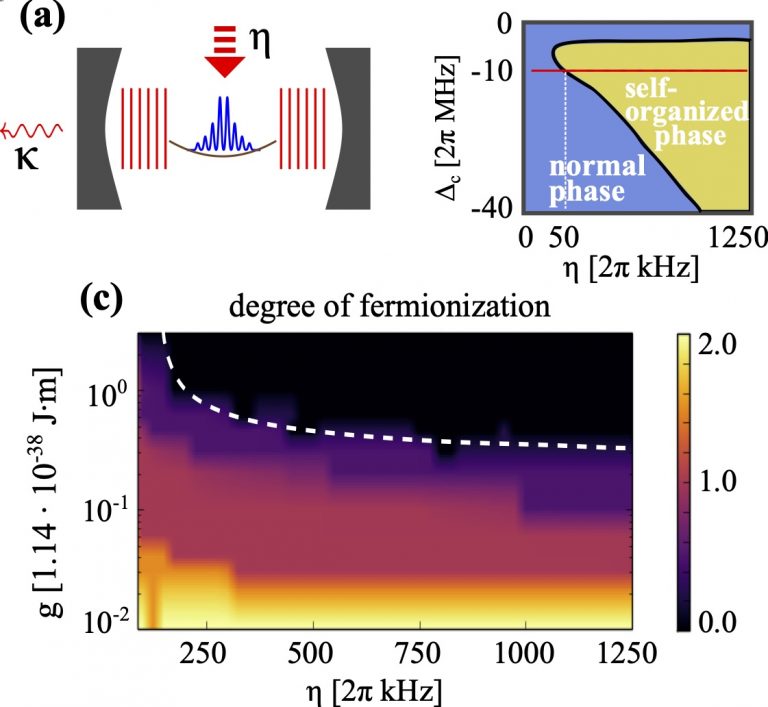
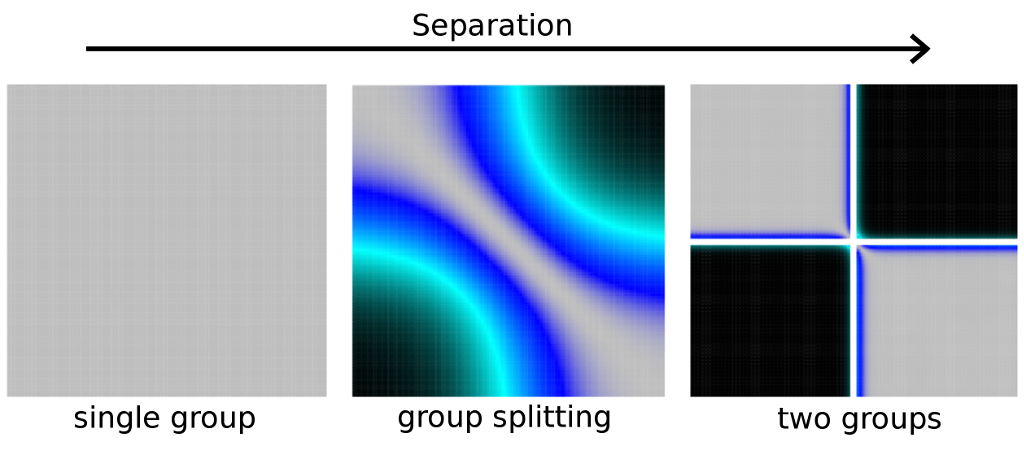
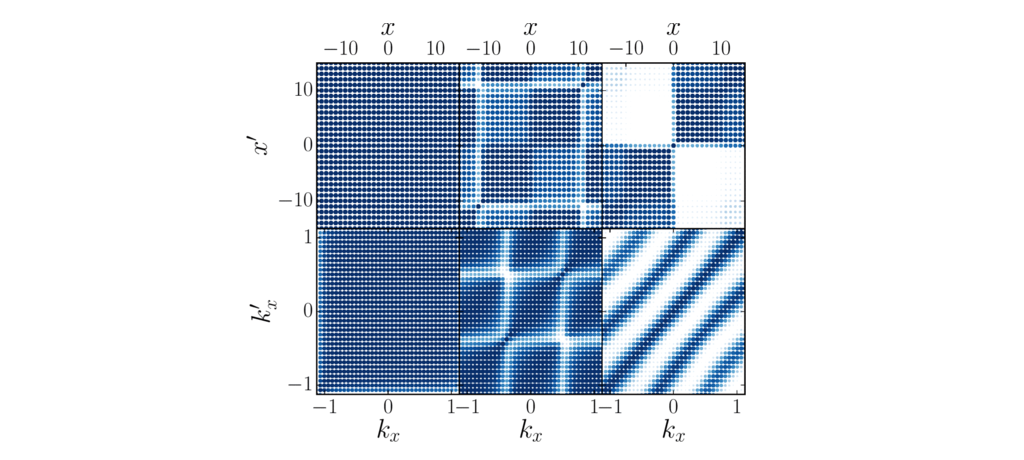
Our paper demonstrates that a quantum simulator for crystal formation is much more flexible when it is built using ultracold dipolar quantum particles. Dipolar quantum particles make it possible to realize and investigate not just conventional crystal structures, but also arrangements that were hitherto not seen for any material. The study explains how these crystal orders emerge from an intriguing competition between kinetic, potential, and interaction energy and how the structures and properties of the resulting crystals can be gauged in unprecedented detail.

Read more at PRL and at arXiv.org .

See this page for the press release and this video with an interview about the paper by its lead author Budhaditya Chatterjee.