Next: Input files for Fig. 2 Up: supp_mat_WEB Previous: Discussion on the convergence
The Hubbard model usually serves as good approximation for a lattice system. It assumes only one Wannier function contributes in each lattice site. We note that the MCTDH-X enables a modelling of the many-body state with an improved accuracy as compared to the Hubbard-lattice-models, because it uses a general, variationally optimized and not necessarily site-local basis set. This improved accuracy is of particular importance in cases where the single-band Hubbard description fails, for instance, due to the action of a blue-detuned cavity [3] or long-range dipolar interactions [5,6,4]. Direct comparisons between the MCTDH-X and Hubbard models have been performed in Refs. [12,9,15,7,8,13,14,16,11,10].
The Bose-Hubbard Hamiltonian takes the following form in one dimension,
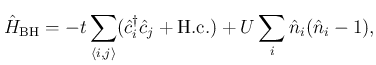 |
(4) |
In the limit
![]() , the system is in the superfluid phase, and the ground state is given by
, the system is in the superfluid phase, and the ground state is given by
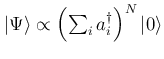 . In this state, the
. In this state, the ![]() symmetry
symmetry
![]() of the system is broken spontaneously, such that all the particles have the same phase. Particles in different sites are coordinated; they are condensed in the same single-particle state. This condensation entails a Glauber one-body correlation between sites which is unity.
In the limit
of the system is broken spontaneously, such that all the particles have the same phase. Particles in different sites are coordinated; they are condensed in the same single-particle state. This condensation entails a Glauber one-body correlation between sites which is unity.
In the limit
![]() , the system is in a Mott insulator phase where the ground state of the system is given by
, the system is in a Mott insulator phase where the ground state of the system is given by
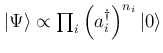 , where
, where ![]() is the number of particles in the
is the number of particles in the ![]() -th site and satisfies the constraint
-th site and satisfies the constraint
![]() . In this state, particles in different sites are disconnected and have no information on each other's behaviors. The phases of the particles in different sites lose coherence. Strong correlation effects build up and the one-body correlation between sites vanishes.
The transition point given in units of
. In this state, particles in different sites are disconnected and have no information on each other's behaviors. The phases of the particles in different sites lose coherence. Strong correlation effects build up and the one-body correlation between sites vanishes.
The transition point given in units of ![]() depends on the structure of the lattice. In particular, it is roughly proportional to the filling factor and the inverse of the dimensionality [17].
depends on the structure of the lattice. In particular, it is roughly proportional to the filling factor and the inverse of the dimensionality [17].
 |
For illustration, we consider ![]() weakly-interacting (
weakly-interacting (![]() ) bosons in a double-well potential with high barrier
) bosons in a double-well potential with high barrier
![]() dw
dw![]() , where the two wells are Mott insulating from each other.
According to the single-band Bose-Hubbard model, the energy of this system is minimzed when the bosons are evenly distributed into the two wells, with three bosons in each well. The many-body state can thus be written as
, where the two wells are Mott insulating from each other.
According to the single-band Bose-Hubbard model, the energy of this system is minimzed when the bosons are evenly distributed into the two wells, with three bosons in each well. The many-body state can thus be written as
 ,
where
,
where
![]() and
and
![]() are the creation operators for the band in the left and right well, respectively. Although such a picture is well supported by the momentum space density distribution and the one-body correlation function [
are the creation operators for the band in the left and right well, respectively. Although such a picture is well supported by the momentum space density distribution and the one-body correlation function [![]() ][cf. Fig. 2(e,f) in the main text], it contradicts with the two-body correlation function [
][cf. Fig. 2(e,f) in the main text], it contradicts with the two-body correlation function [![]() ] obtained from the simulations. In a Mott insulator state where
] obtained from the simulations. In a Mott insulator state where ![]() between lattice sites vanishes, the diagonal term of
between lattice sites vanishes, the diagonal term of ![]() is directly related to the number of particles
is directly related to the number of particles ![]() in the corresponding site through
in the corresponding site through
![]() [16]. If the single-band Bose-Hubbard model holds true, the diagonal term of
[16]. If the single-band Bose-Hubbard model holds true, the diagonal term of ![]() would be uniformly
would be uniformly
![]() since
since ![]() . This is not the case in the simulations when sufficiently many orbitals are used. The landscape of the correlation function is uneven, with values ranging from 0.4 to 0.8 [Fig. S1(b)]. On the contrary, if only
. This is not the case in the simulations when sufficiently many orbitals are used. The landscape of the correlation function is uneven, with values ranging from 0.4 to 0.8 [Fig. S1(b)]. On the contrary, if only ![]() orbitals are used in the simulations, indeed
orbitals are used in the simulations, indeed
![]() holds uniformly [Fig. S1(c)]. These results show that the higher-order (
holds uniformly [Fig. S1(c)]. These results show that the higher-order (![]() ) orbitals are indispensable for correctly capturing the particle correlations, and indicate that more than one mode has contributions in each well. The single-band Bose-Hubbard model is an over-simplification for the system.
We have seen that although the third orbital
) orbitals are indispensable for correctly capturing the particle correlations, and indicate that more than one mode has contributions in each well. The single-band Bose-Hubbard model is an over-simplification for the system.
We have seen that although the third orbital
![]() is two order of magnitude lower than the second orbital
is two order of magnitude lower than the second orbital
![]() , it has significant impact on the simulated particle correlations.
, it has significant impact on the simulated particle correlations.
In summary, to decide whether the convergence in orbital number has been achieved, we should perform simulations with more orbitals and compare the convergence in different quantities of interest.