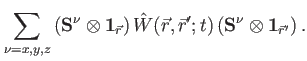Special parameters to treat multi-level atoms and spinors

In order to treat particles that have internal structure, like multileveled atoms or spinor particles, a set of special input variables has been introduced to the above System Parameters Namelist. These define the number of levels, the presence of a conical intersection and whether the interparticle interaction contains a spin-dependent part or not. In principle, a conical intersection amounts to off-diagonal terms in the one-body Hamiltonian $\hat{h}_i^{(CI)}$ which couple the different levels whereas a spin-dependent interparticle interaction means that there is two-particle interactions $\hat{W}_{\mathrm{spin}}$ that can change the spin of particles. These terms read as follows:

$$\hat{h}_i^{(CI),kk} = \left( \hat{T}_i + V_{kk}(\hat{\vec{r}_i}) \right) \otimes \mathbf{1}_{\vec{r}};\qquad \hat{h}_i^{(CI),kj}= V_{kj}(\vec{r}_i)\hat{\pi}_{jk}$$ (3)

$$\hat{W}_{\mathrm{spin}} = \sum_{\nu=x,y,z} \left( \mathbf{S}^\nu \otimes \mathbf{1}_{\vec{r... ...\vec{r},\vec{r}';t) \left( \mathbf{S}^\nu \otimes \mathbf{1}_{\vec{r}'}\right).$$ (4)

Here, the operator $\hat{\pi}_{jk}$ was defined, which makes level $j$ appear in the coordinate space of level $k$ for the spinor orbital on its right. Furthermore, the representation $\mathbf{S}^\nu$ was introduced for the general spin operators in $\nu=x,y,z$ direction. For problems including spin-orbit interactions the folloing Hamiltonian $\hat{h}_{SO}$ is added to the one-body Hamiltonian:

$$\hat{h}_{SO}= \gamma \left[ \alpha \left( \hat{p}_x \mathbf{S}^y ... ...+ \beta \left( \hat{p}_x \mathbf{S}^y + \hat{p}_y \mathbf{S}^x \right) \right].$$ (5)

The parameters $\alpha,\beta,\gamma$ are the prefactor of the Rashba spin-orbit term, Dresselhaus spin-orbit term and the overall strength of the spin-orbit coupling (see also input parameters below). Generally, when the above terms are present in the Hamiltonian, a transfer of population between the different levels of the treated particles is allowed. The input variables necessary to control the program through the MCTDHX.inp file in the case of multileveled or spinor particles are specified in the following table 4.2.

System Parameters Namelist
Parameter	Meaning	Options
NLevel	How many levels do the considered particles have?	Integer, default 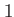$1$.
Multi_level	Do the atoms have internal structure?	Logical, default .F.
Conical_Intersection	Does the one-body Hamiltonian contain terms $V_{jk}(\vec{r})$ that couple different internal states?	Logical, default .F.. If set to .T., the potential VTRAP_EXT which is defined in Get_1bodyPotential.F contains one additional vector that stores $V_{jk}$
InterLevel_InterParticle	Does the interparticle interaction couple different internal states directly (attention: this is for multileveled atoms which are NOT spinors	Logical, default .F.
xlambda<X>	Interparticle-intra-level interaction strength for non-spinors; <X>=1,2,3	Real, default 0.d0 .
xlambda12	Interparticle-inter-level interaction strength for non-spinors;	Real, default 0.d0 .
Spinor	Are the treated atoms spinors with a spin-dependent interparticle interaction	Logical, default .F.
Lambda<X>	spin-independent (<X>=1) and spin-dependent (<X>=2) interparticle interaction strength, respectively, for each level.	Real array, dimension 10, default 0.d0 .
SpinOrbit	Toggles inclusion of spin-orbit-interaction in the Hamiltonian	Logical, default .F.
Rashba_Prefactor	Magnitude of Rashba-spin-orbit-interaction	Real, default 0.d0
Dresselhaus_Prefactor	Magnitude of Dresselhaus-spin-orbit-interaction	Real, default 0.d0
SpinOrbit_Prefactor	Magnitude of total spin-orbit (Rashba + Dresselhaus) term	Real, default 0.d0

It is important to note that it is necessary to specify at least as many one-body potentials as there are levels or spinor components in the treated particles. In the case of atoms featuring a conical intersection, the number of potentials is NLevel + 1. This is done in the routine Get_NLevelPotentials in the Get_1bodyPotential.F source file. The available predefined multilevel potentials are collected in the following table 4.2.

whichpot	Description	Potential	Parameters
HO1D	Parabolic potentials with different frequencies and offset for different spin components or levels. This potential is defined for two-level or spin- $\frac{1}{2}$ atoms, only.	$V_{\uparrow}(x)= \frac{1}{2} p_1^2 x^2;$ $V_{\downarrow}(x)= \frac{1}{2} p_2^2 (x-p_3)^2+p_4$	$p_1,p_2$ are the frequencies of the $\uparrow,\downarrow$ components/levels, respectively. $p_3$ is the horizontal displacement of the two parabolas and $p_4$ their relative offset.
linearZ1D	Parabolic optical confinement with linear Zeeman shift and a spatially homogeneous magnetic field in one dimension.	$V_{m_F}(x) = \frac{1}{2} p_1^2 x^2 + m_F p_2 \vert x \vert$	$p_1$ is the frequency of the optical confinement and $p_2$ defines the magnetic field strength.