Column 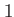 to to 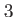 |
Column 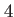 |
Column 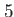 to to
 |
Column
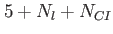 & &
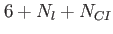 to to
 & &
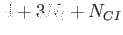 |
Column
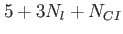 & &
 to to
 & &
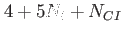 |
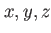 |
DVR weight |
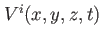 and and
 |
 |
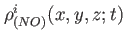 |
Column
 & &
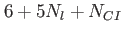 to to
 & &
 |
Column
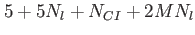 & &
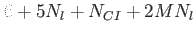 to to
 & &
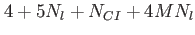 |
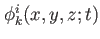 for for
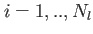 and and 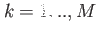 |
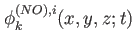 for for
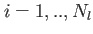 and and 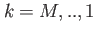 |
This table explains the column structure of the <time>orbs.dat output files of the main or analysis program for the case that Multi_Level=.T. was set. 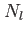 is the number of internal states and is the number of internal states and 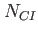 is the number of conical intersections ( is the number of conical intersections (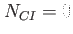 if Conical_Intersection=.F.). Please note, that the index of the internal state is always running first before the orbitals' index. if Conical_Intersection=.F.). Please note, that the index of the internal state is always running first before the orbitals' index. 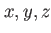 are the spatial coordinates, are the spatial coordinates,
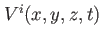 is the one-body potential of internal state is the one-body potential of internal state 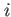 , ,
 is the coupling of the is the coupling of the 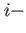 th conical interaction, th conical interaction,
 is the density in working orbitals for internal stat is the density in working orbitals for internal stat 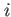 , ,
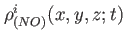 is the density in natural orbitals for state is the density in natural orbitals for state 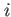 , ,
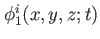 to to
 are the working orbitals in internal state are the working orbitals in internal state 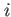 , and , and
 to to
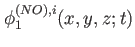 are the natural orbitals in state are the natural orbitals in state 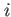 . Please note, that some of
the quantities are complex numbers which then are output decomposed in their real and imaginary parts in two columns (as specified by the column numbers). . Please note, that some of
the quantities are complex numbers which then are output decomposed in their real and imaginary parts in two columns (as specified by the column numbers).
|