Table 20:
Predefined potentials and parameters.
| whichpot |
Description |
Potential |
Parameters |
| HO1D |
 D harmonic oscillator D harmonic oscillator |
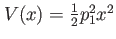 |
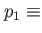 trap frequency. trap frequency. |
| HO2D |
 D harmonic oscillator D harmonic oscillator |
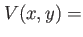
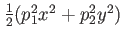 |
 trap frequency in trap frequency in  |
| HO3D |
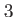 D harmonic oscillator D harmonic oscillator |

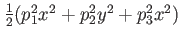 |
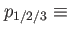 trap frequency in trap frequency in  |
| h+d |
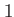 D harmonic oscillator plus Gaussian central barrier D harmonic oscillator plus Gaussian central barrier |
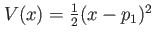
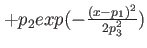 |
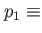 diplacement, diplacement, 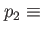 height of Gaussian, height of Gaussian,  width of Gaussian width of Gaussian |
| h2D+d |
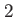 D harmonic oscillator plus Gaussian central barrier D harmonic oscillator plus Gaussian central barrier |
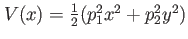
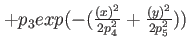 |
 trap frequency in trap frequency in 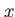 -/ -/ -direction, -direction,  height of Gaussian, height of Gaussian,
 width of Gaussian in direction width of Gaussian in direction 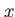 / / |
| HO<X>D+td_gauss |
<X>D harmonic oscillator plus time-dependent [height 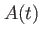 ] Gaussian central barrier in ] Gaussian central barrier in 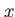 -direction -direction |
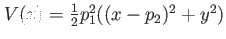
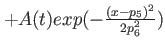 |
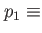 trap frequency in trap frequency in 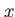 - and - and  -direction, -direction, 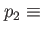 displacement of the minimum of the trap w.r.t. the barrier, displacement of the minimum of the trap w.r.t. the barrier, 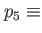 displacement of Gaussian w.r.t. displacement of Gaussian w.r.t.  , ,
 width of Gaussian barrier in direction width of Gaussian barrier in direction 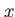 . Height . Height
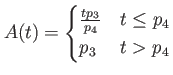 |
| Tilt |
Tilted triple well potential |
 |
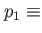 tilt parameter, tilt parameter, 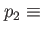 depth of the wells. depth of the wells. |
| Tiltinit |
single well potential to initialize system for a propagation in the tilted triple well potential Tilt. |
![$ V(x) = V(x)=-p_1 x + p_2 \sin(2 x)^4 + [(x-\frac{p_3 \pi}{2})/0.7]^{20}$](img222.png) |
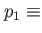 tilt parameter, tilt parameter, 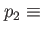 depth of the wells, depth of the wells,  is used to select displacement from the origin. is used to select displacement from the origin. |
| OL_HW_1D |
lattice in one dimension with hard wall boundaries |
 |
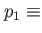 depth of lattice, depth of lattice, 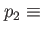 frequency of lattice, frequency of lattice,  are the boundaries for the hard walls. are the boundaries for the hard walls. |
| TDHIM |
Harmonic potential with time-dependent frequency for benchmarks with the time-dependent harmonic interaction Hamiltonian. |
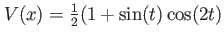
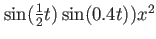 |
No parameters, use with which_interaction ='TDHIM' |
| tun |
Potential for tunneling to open space dynamics |
 |
no parameters, initial wavefunction should be localized at  , use whichpot='ini' for relaxation of initial state. , use whichpot='ini' for relaxation of initial state. |
| thr |
Tunneling to open space with a threshold |
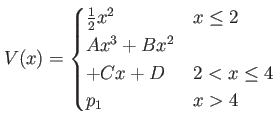 |
Parameter 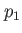 defines the threshold and the polynomial coefficients defines the threshold and the polynomial coefficients
 , ,
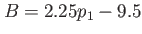 , ,  , ,  . . |
| DQD |
Double quantum dot potential |
 |
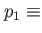 depth of first quantum dot, depth of first quantum dot, 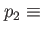 width of first quantum dot, width of first quantum dot,  distance of the two dots, distance of the two dots, 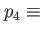 depth of second quantum dot, depth of second quantum dot, 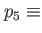 width of second quantum dot. width of second quantum dot. |
| DQDLASER |
Double quantum dot potential illuminated by a laser with time-dependent amplitude
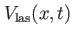 . . |
 |
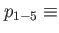 same as in DQD, same as in DQD,
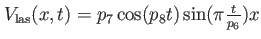 for for 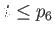 and and
 else. else. |
| zero |
No potential |
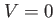 |
No parameters. Boundary conditions determined by the discrete variable representation. |
| MQT_ini |
Rectangular 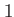 D box D box |
![$ V(x)=\infty \qquad \forall [x\notin (0,20-p_1)]$](img242.png) and and
![$ V(x)=0 \qquad \forall [x\in )0,20-p_1(]$](img243.png) |
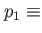 barrier width in propagation MQT_prop barrier width in propagation MQT_prop |
| MQT_prop |
Rectangular 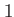 D box, barrier and open space D box, barrier and open space |
![$ V(x)=\infty \qquad \forall [x < 0]$](img244.png) and and
![$ V(x)=0 \qquad \forall [x\in )0,20-p_1(]$](img243.png) and and
![$ V(x)=0 \qquad \forall [x>20]$](img245.png) and and
![$ V(x)=0.05 \forall [x\in (20-p_1,20)]$](img246.png) |
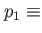 barrier width barrier width |
| qpl |
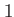 D lattice with D lattice with 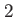 frequencies/amplitudes frequencies/amplitudes |
 |
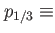 amplitudes of the lattices, amplitudes of the lattices,
 frequencies of the lattices. frequencies of the lattices. |
| rot2D |
 D harmonic oscillator with rotating anisotropy D harmonic oscillator with rotating anisotropy |
 |
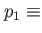 the rotation frequency, the rotation frequency, 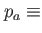 the time-dependent anisotropy. the time-dependent anisotropy. 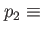 anisotropy maximum, anisotropy maximum,  ramp-up and ramp-down time of the anisotropy, ramp-up and ramp-down time of the anisotropy, 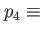 plateau time at which plateau time at which 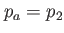 . . |
| stir2D |
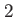 D harmonic trap with rotating stirring rod D harmonic trap with rotating stirring rod |
![$ V(x,t) = \linebreak\frac{1}{2} (x^2 + y^2)+ \linebreak p_3 exp[ \linebreak -\frac{1}{p_4}(x-p_2\cos(p_1 t))^2 + (y - p_2\sin(p_1 t))^2]$](img253.png) |
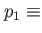 stirring frequency, stirring frequency, 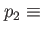 stirring radius, stirring radius,  height of Gaussian rod, height of Gaussian rod, 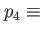 width of Gaussian rod. width of Gaussian rod. |
| ellipse2D |
Elliptic two-dimensional hard-walled potential well |
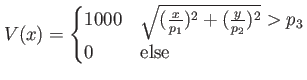 |
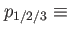 parameters defining the ellipse. parameters defining the ellipse. |
|
|
|
|