| Which_Interaction and Interaction_Type |
Description |
Potential |
'gauss' and 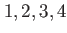 |
Gaussian interparticle interaction of width Interaction_Width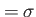 |
 |
| 0 |
Contact interaction with constant strength  |
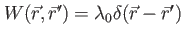 |
'cos' and 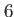 |
Contact interaction with time-dependent strength
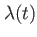 |
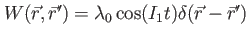 |
'sin' and 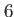 |
Contact interaction with time-dependent strength
 |
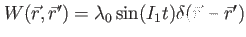 |
'TDHIM' and 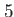 |
Time-dependent version of the harmonic interaction model |
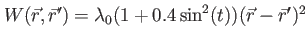 |
'TDgauss1' and 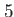 |
Gaussian interaction with width Interaction_Width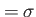 and time-dependent amplitude and time-dependent amplitude |
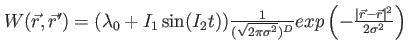 |
'TDgauss2' and 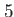 |
Gaussian interaction with width Interaction_Width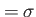 at at  that is time-dependently modulated that is time-dependently modulated |
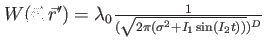
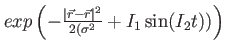 |
'lennart_j' and  |
 - Screened Lennart-Jones potential - Screened Lennart-Jones potential |
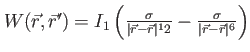 for for
 and and
 for for
 |
'HIM' and  |
Harmonic interaction model |
 |